RECURSION, RABBITS and FIBONACCI

Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem (as opposed to iteration).  Most computer programming languages support recursion by allowing a function to call on itself.

A common computer programming tactic is to divide a problem into sub-problems of the same type as the original, solve those sub-problems, and combine the results.  This is known as a divide-and-conquer method.  The job of the recursive cases can be seen as breaking down complex inputs into simpler ones.  In a recursive function, with each recursive call, the input problem must be simplified in such a way that eventually the base case mush be reached.  A base case would be like reaching the bottom of the stairs (if you started from the top and and the stairs weren't endless).  After reaching the bottom of the stairs, we will make our way back up to the top, one step at a time.  The following is a brief story about Fibonacci, rabbits and an example of a recursive method done in objective-c. 

Fibonacci, also known as Leonardo of Pisa, invented the Fibonacci sequence while studying rabbit populations.  Assuming a newly born pair of rabbits, one male, one female, are put in a field; rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits; rabbits never die and a mating pair always produces one new pair (one male, one female) every month from the second month on.  How many pairs will there be in one year?  How many pairs will there be in 10 years?  The answer to those questions are now referred to as the Fibonacci numbers or Fibonacci sequence.  At the end of the nth month, the number of pairs of rabbits is equal to the number of new pairs (which is the number of pairs in month n - 2) plus the number of pairs alive last month (n - 1).  This is the nth Fibonacci number.  This is the Fibonacci sequence in mathematical terms:

Fn = Fn-1 + Fn-2

What if we wanted the 6th Fibonacci in this sequence, how would we get it?  With computers, we no longer need to reference rabbit love making to come up with that number.  One way is using the recursive function where we will write a method (in this example, using Objective-C) where it will call on itself multiple times in producing whatever number we pass into it.  If we want the 6th Fibonacci number, we will pass 6 in as number in this method.  But what if we wanted the 2,000th Fibonacci number?  Using a recursive method like this would be highly inefficient.  As there are optimal ways of writing a method to produce the nth Fibonacci number (which are clearly more efficient than this recursive function), I am showcasing this particular method to give an example of what a recursive function looks like and how it behaves.  One better way to solve this problem would be to store the Fibonacci numbers in an array where the next item in the array will always equal the sum of the previous two items.

- (NSInteger)findFiboNumber:(NSInteger)number {
  if (number <= 1) {
    return number;
    }
  else {
    return ([self findFiboNumber:number - 1 ] 
           + [self findFiboNumber:number - 2]);
    }
}

This method will return a NSInteger number.  The argument to this method (which is of type NSInteger) will be where we pass in the number 6.  What will be returned after all is said in done, will be the number 8.  Below is a visualization of how we get to 8 after passing in 6.

RECURSION TREE
a visualization of the recursion method written above

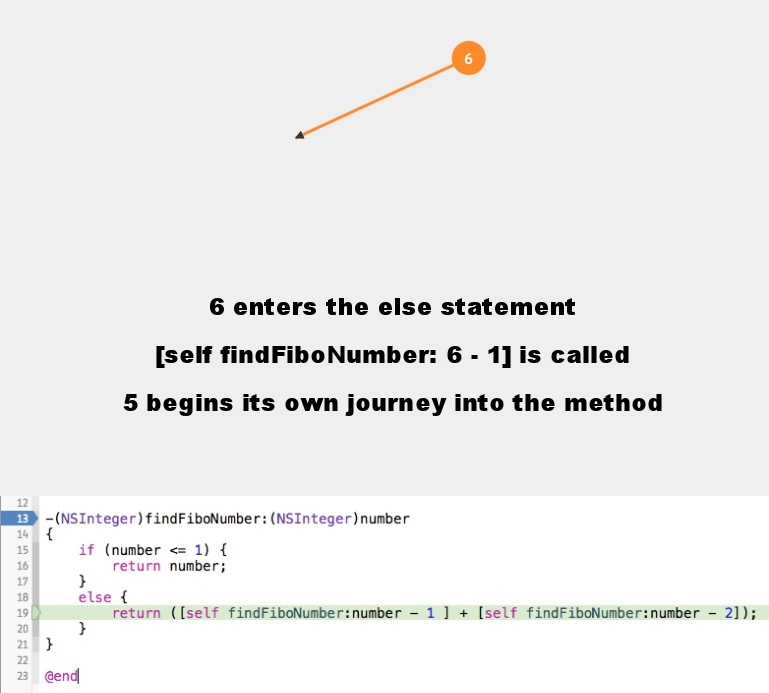
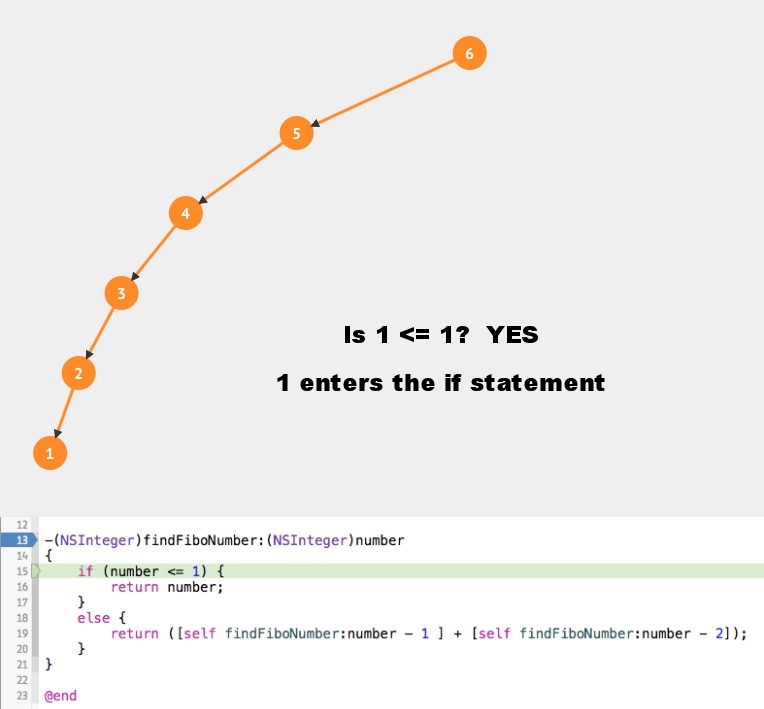
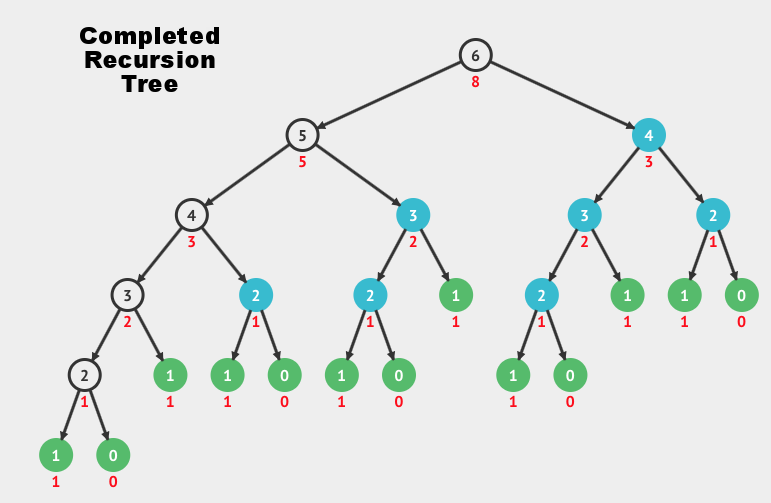
• The circled numbers represent what figures are being passed through the method (at various stages).
• The red numbers below the circled numbers represent what figures are being returned.
• The final returned number is 8 (the red figure below the circled 6 which began the method).